Dave MacEwen's Blog

The Origins Of The Musical Scale From Pythagoras To Equal Temperament Featuring Auditory Illustrations and Comment

Introduction to Music

Theory

1. Have you ever wondered where musical scales came from?  Why are scales built around octaves  and why are there only seven different notes?   I mean there are 88 different keys on a piano but really there are just 12 different notes counting the black keys.  Those 88 key are actually divided up into about 7 octaves, each octave comprised of just those 12 noters.  But each successive octave is double the frequency of the one it proceeded.   Who came up with the idea of musical scales in the first place?  What did they sound like, were they any different than the ones we use today?  There are some strange things about scales.   Most of the notes are separated by what are called whole steps but two of the intervals are shorter – why?  And on a piano, why are the black keys given two names?   For example the C-sharp or D-flat key, it only produces one tone.
2. I will try to answer these questions and many others about the origins of today’s musical scales.  When possible, I will  provide audio files to illustrate the points I’m making.  I’ll tell you about some of the many problems that occurred with these scales.   In the telling, I will  share major developments throughout the history of western music.  I think you will find this history  fascinating – especially if you happen to love music!  When you are finished you will have learned much about what is referred to as music theory that can be applied from Bach to Taylor Swift.  I want to emphasize that knowledge of music theory was not necessary for musicians to produce beautiful music.  But music theory has none-the-less provided a structure for music composition and a way to formalize this most abstract of human arts.
3. Probably the best way to understand the development of musical scales is to first get some idea of the nature of sound especially musical sound.  Our experience of sounds has a physical correlate in vibrations.  The source of any sound  must freely vibrate.   I’ll illustrate with a couple of examples.
4. A tree falls in the forest.  When it hits the ground the tree  vibrates.  The vibrations disturb the surrounding air molecules .  Like little ping pong balls banging together,  pushed back and forth by the vibrating tree.   These waves of molecules set up a chain reaction that moves out away from the tree  like  waves moving out from where a pebble has been thrown into the water.  The waves move out further and further  eventually losing energy and die out.
5. A tuning fork’s  vibrating tines disturbs the air molecules.  A bowed violin string  likewise sets up traveling waves.   The vibration pattern of the tree are uneven and jagged-looking.  Those of the tuning fork or violin string even and smooth.  The tree produces potential noise, the tuning fork and violin string music-like sounds!
6.   This little graph illustrates what I mean.  The musical sound has vibrations that are even, those of noise are random and uneven.    
7. The musical vibration is termed a ‘sine wave’ while the noise vibration is just termed ‘noise.’
8. missing in all of this is a listener.  Without a listener there is no sound – only waves from vibrations.
9. The listener is equipped with a marvelous system to ‘hear’ sounds from these waves.  Call them sound pressure waves.

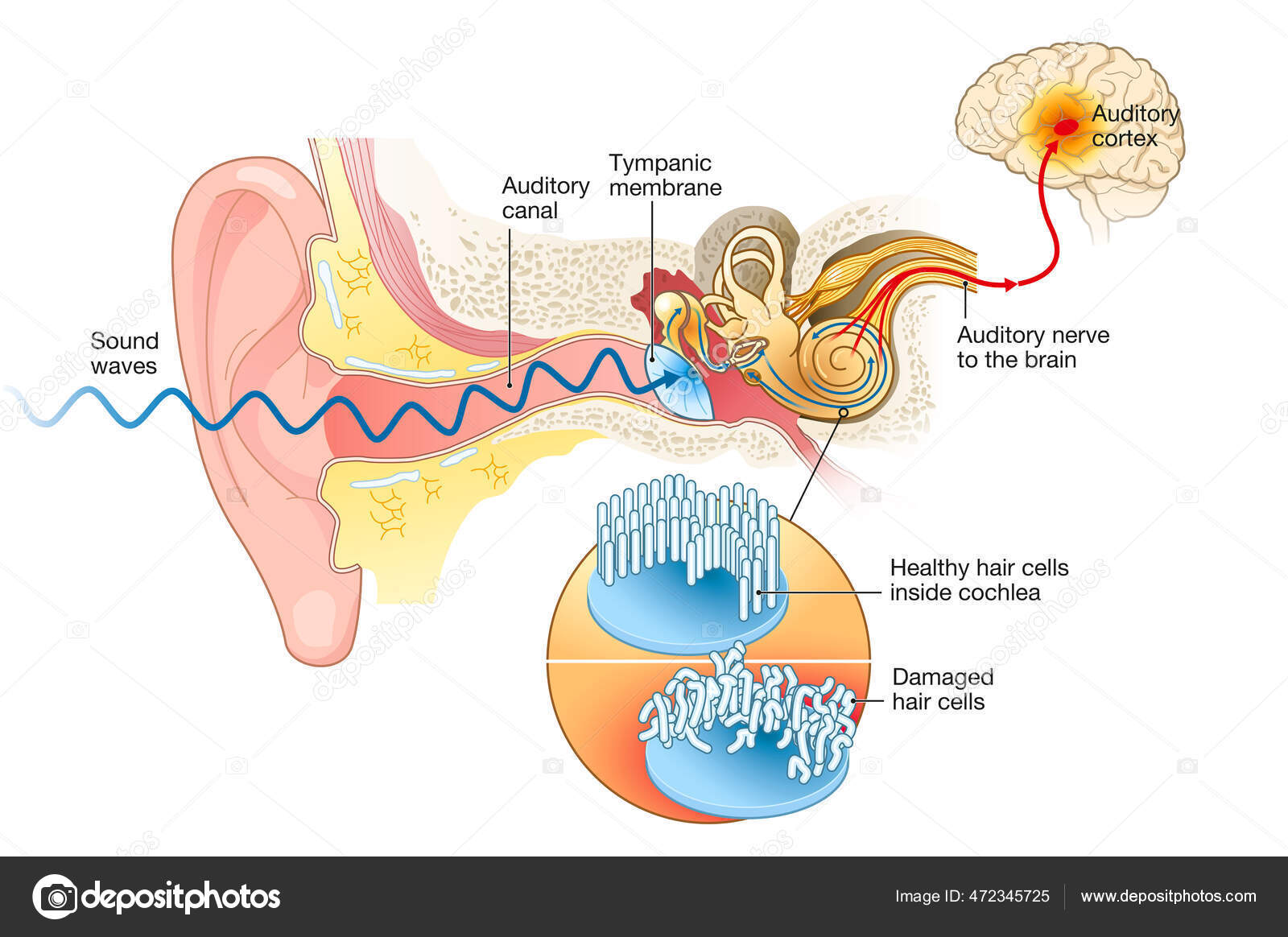
1.  This little diagram shows the human ear.  It is a supreme instrument, the work of millions of years of evolution.
2. If the person is in the vicinity of a burst of  sound waves as described above, the waves produce pressure that reaches  inside of the ear canal.  As a wave , the pressure ebbs and flows in the ear canal and sets up  sympathetic vibrations of the ear drum or  ‘tympanic membrane.’
3. Sitting in fluid behind the ear drum are three of the smallest bones in the human body: ‘hammer’, ‘anvil’, and ‘stirrup;’ together known as the ossicles.  The incus malleus, the hammer, is attached to the ear drum.  Vibrations of the ear drum set up correlated back and forth movements in the ossicles.

1. The ear drum pushes against the hammer resulting in the stirrup pushing against another drum-like membrane termed the oval window.
2.  
3. The movement of the oval window causes hair cells to stretch in a mysterious organ buried deeply within the mastoid bone behind the ear.  This organ is the cochlea, coiled and looking similar to a snail from the outside.  Inside, the hair cells are arranged similar to a harp or piano receiving high frequencies and one end and low frequencies at the other.  The stretching of these hair cells produces electrochemical signals that reach the brain and we experience sound.  This process  of hearing sounds is as yet unknown to us.  There energy from vibration produces sound pressure energy that enters the ear.  This energy produces movement in the ossicles that stretch the neural hair cells in the cochlea. The energy from this movement is transduced into electrochemical energy that forms the information that reaches the brain over nerve branches.  This energy information is ‘processed’ by the brain and bingo, we experience sound.  But by ‘processed’ I might as well say ‘presto’ or something magical sounding because at this point we have no understanding of how ‘sound’ happens!

4. The Musical Sound Wave

5. The violin string when bowed or plucked produces a vibration that has a particular form.  I showed that form above but  over simplified.  Vibrations that sound ‘musical ‘ produce   complex waves which I’ll explain in a moment.  But perhaps first this may be a good time to introduce one of the stars of my story.  He was a famous mathematician, philosopher, and teacher from Ancient Greece.  His name was Pythagoras.  If you went to school almost anywhere in the world  you undoubtedly got introduced to him.  Most likely, unless you were a philosophy major, your first  introduction to Pythagoras was the Pythagorean Theorem.  The length of the hypotenuse of a right triangle can be determined as the sum of the squared lengths of the other two sides.   But Pythagoras was famous for many things.  He lived in Greece 500 years before the date of the birth of Christ.  Unfortunately, he left no written work.  But he had many disciples who  wrote about him.  They attributed many things to Pythagoras but sadly there is no concurring proof for most of it- we just don’t know.  He was certainly an extraordinarily knowledgeable mathematician.  And like other mathematicians of his time he was obsessed by ratios.  They were the golden measure.  To Pythagoras all of nature, including the known universe at the time, was composed of ratios.  To Pythagoras ratios were not mere numerical values, they were metaphysical; magical.  Humans were believed to relate to them.  Small concise ratios were responded to in a very positive way.  Large cumbersome ratios not so much.  This will be important as we explore the Pythagorean Tuning for the first musical scale.
6. It is very likely that Pythagoras played the Lyre.  As a scientist he asked many questions.  He  must have been curious about the musical sounds  of his Lyre.  So, like a good scientist, he experimented with strings.  By bowing or plucking them it was obvious they vibrated.  What did he learn from the vibrating string?

Pythagoras had at his disposal a  monochord.  

It had one string stretched out tightly with a means to depress it at various loci along its length.  These were called nodes.  Without depressing the string, he plucked it and it produced a musical sound as it vibrated along its entire  length.  He discovered that if he then depressed the string right in the middle, the  two equal halves vibrated twice as fast as before and sounded exactly one octave higher.  It is not completely clear if he focused on the vibrations or simply the changing lengths of the string.   The results are inversely correlated.  Then, most likely by trial and error, he depressed the string exactly dividing it into into thirds.  This produced a musical tone a perfect fifth from the original tone.

1. So far, Pythagoras produced three tones: the original tone; the octave; and the perfect fifth.  He was struck by the ratios of these lengths to that of the full string: 2 to 1 ==> the octave and 3 to 2 ==> the perfect fifth. 
2. These musical intervals sounded quite pleasant or ‘consonant’ to the early Greeks.  Indeed, the music of that time was surprisingly simple consisting mostly of these three notes along with a perfect fourth which  I will describe in a moment.

The Experiment

1. Lets’ recreate Pythagoras’ experiment.  Instead of a monochord I’m going to use a simple ukulele.   One of the strings is 34 inches in length.  First I pluck it and you hear a musical tone which my tuner tells me is a G.  Now, I measure down half the length of the string at a point 17 inches from the bridge and depress the string.  I pluck the string again and it sounds pleasant and very much like the tone earlier only higher.  My tuner tells me the tone is also a G an octave higher.  Pythagoras’ law: the pitch of a musical note is directly proportional to the length of the string.  Halve the length of the string doubles the pitch; it sounds twice as ‘high.’  We have created an octave.  Listen to it below.  

If you have a uke or guitar lying around try it yourself.

Now let’s create a perfect fifth to the original G. Using the G string on the Uke I first pluck the string to produce a G tone. Then I mover down one-third the length of the string, 11.3 inches, and depress it at that point and pluck the string. The tone that sounds is the perfect fifth up from G. That note is a D. Then I release the string and again pluck it to sound the G. Listen below.

The relative lengths of the string for the two notes is 3 to 2 (34”/22.5” approximately 1.5). Pressing the string a third of the way down, or rather, up its length, divides it as one-third, two-thirds.

These three notes/tones plus one more, pretty much exhausts all of the notes the ancient Greeks at the time of Pythagoras utilized in their simple music! They must have had rather persnickety tastes. Interestingly, musical instruments that date back 10 thousand years earlier were designed to play many more notes that those favored by the Greeks of Pythagoras’ time. Lets’ produce one more note the Greeks used, termed the ‘perfect fourth,’ The ‘fifth’ and ‘fourth’ designation were not from the Greeks. Much later in history these numbers referred to the sequential position of the notes relative to the fundamental note referred to as the ‘tonic.’

So far the length ratios of the notes are: 2 to 1 for the octave and 3 to 2 for the perfect fifth. The ratio for the perfect fourth is 4 to 3. Pythagoras depressed the string one-fourth of the way up essentially dividing it into fourths. Lets’ hear what it sounds like on the uke string. I will depress the uke string 6.5 inches up from the bridge. Listen below.

Now, you hear the perfect fourth. When the G is the tonic, as it is here, the perfect fourth is the high C. In today’s musical parlance the perfect fourth is called the ‘sub-dominant’ while the perfect fifth is termed the ‘dominant.’ Listen below as I pluck G C G. This is one of the most common progressions in western music as it was during Pythagoras’ time.

Lets’ see if we can hear the four notes we’ve created.

Several things to note here. The Greeks perceived the note combinations of the octave, perfect fourth, and perfect fifth along with the tonic note, as pleasing or ‘consonant.’ Other combinations one might come up which were thought to sound ‘harsh’ or dis-consonant. And, most importantly for Pythagoras, the ratios of the lengths of the string for these various notes were small and simple, just as he predicted they would be.

Pythagoras’ Rationale for His Musical Scale

If the octave and the perfect fifth are the most consonant sounding musical intervals, then why not construct a musical scale made up exclusively from them? Maybe throw in a few perfect fourths for good measure. This is what he did. I am assuming that he utilized ratios of string length to compete his musical scale. Maybe, he knew more about string vibration than we think and he used vibration ratios to complete the scale. I’m guessing he utilized only his monochord and string length.

To simplify things lets’ change the tonic from G on the ukulele to C. The ratio of the lengths of the strings for each perfect fifth should ideally, always stay constant at 1.5. Let me write the notes so far in terms of their lengths. Let L be the length of the tonic note string.

C = L F = 4/3L G = 3/2L C’ = 2L.

But Pythagoras wanted more than just 4-note. Hows many? Well, he was constrained by the size of the octave itself and each new note must be a perfect fifth from its nearest neighbor. So how many notes fit within an octave? The interval between F and G would have the ratio 3/2L divided by 4/3L or 9/8L called a major second or whole tone. (Divide ratios to get their difference). So, a note immediately above the tonic C must be 9/8L, i.e., one whole tone above C. That note D, becomes the second note of the scale. Then, the next note up must have a string length of (9/8)^2 L, two whole tones above C. This note, known as the ‘third’ is E on the scale.

The interval between E and F must be 81/64L ((9/8)^2) divided by 4/3L which is 256/243L. This is the first semitone and look how large the ratio is and how narrow the interval. Pythagoras could not have been happy with this large and unappealing ratio! The next two notes are F and G, the sub-dominant and dominant, and we’ve already determined their string lengths. The note above G is constrained to have a string length of 3/2L * 9/8L or 27/16L, The next note is the important major seventh, C to B and B should have a string length of 27/16L * 9/8L or 243/128L. This must have been another ugly ratio for poor Pythagoras and contributes to the second semitone B to C’ with a ratio of 256/243. The last note is C’ an octave above with a string length of 2L. The separation between notes of a hemitone is smaller than that for a whole tone: (256/243)^2 < 9/8. This alone makes Pythagoras’ diatonic scale sound different than that from modern tuning which we’ll get to a bit later on.

The 8 notes above comprise Pythagoras’ the diatonic musical scale. The diatonic scale was later augmented by adding tones between notes separated by a whole step. This expanded the number of notes available to the composer but led to the problem discussed earlier that C# had a slightly different frequency vibration, Hertz, than D-flat.

Caveat

Of course, no one will ever know how Pythagoras arrived at his final musical scale. He wrote nothing, we are left to depend on his many disciples who wrote about him often decades, even centuries after his death. I recreated how it would be possible to devise a musical scale utilizing just string length. Since we have a record of his monochord and assume he was not familiar with the science of string vibrations and tone, it seems reasonable to assume he used such a procedure.

The arrangement of these 8 noters, all equally spaced save between E to F and B to C, is termed the ‘Diatonic Scale.’ It was the first attempt to construct a musical scale based on a combination of experimental results in human perception and Pythagoras’ metaphysical beliefs concerning ratios. The scale was as good and complete as was possible then – it featured the octave and contained four perfect fifths and five perfect fourths. No other selection of eight notes can possibly produce anything more concordant. It also provided a sufficient number of notes with which to compose songs of beauty and interest. This scale and the 12 note scale that followed endured well into the Renaissance centuries later. What more could be asked ? Well, you’ll find out a little later on but before that I want to point out why Pythagoras’ musical scale generally sounded so pleasant.

Listen to Pythagoras’ Diatonic Scale. I have included below Pythagoras’ and the modern version of the diatonic scale termed 12-TET. Can you tell any difference? It takes quite a trained musical ear to do so unless you are one of those rare individuals with ‘perfect pith’ able to detect the slightest differences in frequencies.

Pretty hard to hear much difference though perhaps you heard some. I’ll have much more to say about the modern 12-TET scale later. Perhaps you heard the slight difference between the Pythagoras hemitone and the half-tone of the modern diatonic scale. Recall that the hemitone is the more narrow interval but perhaps not enough to be easily perceptible. Below I’ve added the Pythagoras hemitone between E and F followed by the 12-TET half tone between E and F. Then follows the hemitone between B and C and the same interval using the half tone of the modern 12-TET.

Again, pretty difficult to detect frequency differences of roughly 9 Hertz between the two types of scales. I’ll explain later about measuring frequency differences in what are termed ‘cents.’

Overtones or Frequency Harmonics

Earlier I oversimplified the vibration pattern generated by a plucked string. Yes, it does vibrate in an even pattern known as a sine wave as illustrated in the little figure I presented. But it is considerably more complex. A musical vibration from say a harp string consists not only of the fundamental sine wave frequency but many secondary frequencies. These secondary frequencies are ordered in a harmonic series of the form 1/n. First, there is the primary or fundamental frequency measured by counting the number times the wave completes one cycle in one second. This measure is the Hertz value of the frequency. For example, middle C on a piano has a fundamental frequency of 261.6 complete cycles per one second.

There is a secondary frequency which accompanies the fundamental frequency. Recall Pythagoras’ monochord with a single string anchored at each end. Let’s say it vibrates 261 times per second. At the same time imagine there is a node right in the middle forming two wave patterns each vibrating twice as fast as the original fundamental frequency. This arrangement produces a tone exactly one octave higher than that of the fundamental frequency.

As you see in the figure above there is yet a third frequency formed from two nodes dividing the string into thirds. Then a fourth frequency with three nodes. And a fifth and a sixth frequency and so forth. These additional frequencies are part of an endless harmonic series. Though each succeeding frequency is reduced in volume proportional to 1/the number of nodes, around the fifth frequency the sound is barely audible.

The musical tone is a wave of waves. These secondary waves produce ‘timbre‘ giving the tone a particular richness unique to any given combination of overtones. It is the timbre that makes a clarinet sound like a clarinet, a trumpet sound like a trumpet and the ukulele sound like a ukulele . For example, the clarinet produces a harmonic series of only even numbers.

Though he was most likely unaware of overtones or harmonics, you probably discovered for yourself the relation between the harmonics and the octavos, perfect fifths and fourths making up Pythagoras’ musical scale. The ratios between the fundamental frequency and second, third, and fourth harmonics are the same as those making up Pythagoras’ octave, perfect fourth and perfect fifth. These ratios are small and the intervals are perceived as pleasant. The only exceptions are the hemitones.

The Octave

Pythagoras constructed his musical scale to conform to an octave. Why did he do this? The answer may come from the fact that the octave provides a framework that structures our perception of music.

Listen to the following section from a piano piece by Arnold Schoenberg a 20th century composer who developed a scale known as the 12-tone row. All 12 notes of the modern musical scale must be played before repeating any other note. The idea was to produce ‘atonality.’ That is, a melody with no particular key – no note serving as the ‘tonic note’ grounding as it were the melody. The music was generally a flop save some of his students and a few musical academics. One of his students, Alban Berg did go on to acclaim and his opera Lulu was a giant success and is still performed. People just seem to need the structure and foundation provided by placing a melody within a key defined by the octave. All of the evidence available to musical scholars indicates that this need for a key structure and a melody defined within an octave is universal; spanning all known cultures. Take a listen to Schoenberg below and see what you think.

Some more popular artists also made attempts at songs designed to be atonal. One of the most popular was a song by David Crosby of ‘Crosby Stills and Nash’ called ‘Guinevere.’ He tuned his 6-string guitar from the normal E A D G B E to D A G D B E producing an etherial-like quality to the song and distorting any notion of a key for the melody. Listen to a snippet of ‘Guinevere’ by Crosby and the Lighthouse band recorded just a few years ago. Cosby died not long after the recording leaving the world absent a great talent. Take a listen to ‘Guinevere’ below. Joanie Mitchell also tried her hand at at atonality with her song ‘Chelsey Morning’ by tuning her guitar similarly.

The octave has played a role directly in the melodies of many famous songs. Below are just a few.

Many popular songs start out with a melody that jumps the whole octave. Listen to two examples of so many I could have selected from. The first is the famous Thus Spake Zrathustra by Richard Strauss. The second is equally famous and recognizable, Over the Rainbow here sung by Judy Garland from the 1939 movie. The melody starts immediately with an octave jump.

So, kudos to Mr. Pythagoras! He gave us our first formal musical scale and built it around the octave. This format hasn’t changed for over two millennia.

Unfortunately, despite the genius work that went into the development of the first musical scale there was an Achilles heel, known as the dreaded Pythagoras Comma.

The Pythagoras Comma

The driving force behind the musical scale of Pythagoras was to produce a scale with a sufficient number of notes to compose songs and musical intervals that were as consonant as possible. And all of this placed within an octave. Unfortunately, things don’t always go as they should, even for Pythagoras. I will try to make as clear as I can the serious problem Pythagoras faced.

A helpful little diagram can perhaps introduce the issue facing Pythagoras. Recall again, Pythagoras constructed his scale based on the fact that the interval of the octave and the perfect fifth were considered at the time the most consonant and pleasing to hear. Let’s consult a musical clock made up of notes separated a perfect fifth apart.

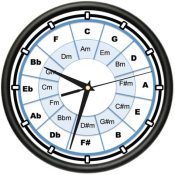
The notes corresponding to the hours are perfect fifths apart. Starting at 12 o’clock is C followed by G forming an interval of a perfect fifth. Then successive perfect fifths D A E B … around the clock. Going counter clockwise we’d also produce notes a perfect fifth apart. Going either way completely round the clock we would span 7 octaves, from C to C. Remember that an octave is defined as the interval between two notes with a frequency ratio of 2 to 1. The upper note of that octave will be twice the frequency of the lower note.

Going from C to C round the clock for 7 octaves ends up at a note 128 times the frequency of the starting C. In general this would be (2^7)F = 128F, where F is the starting frequency at 12 o’clock. But the math doesn’t accurately describe what happens. There are 12 such perfect fifths round the clock. So, that makes ((3/2)^12)F since there are twelve such perfect fifths. This works out to be 129.74F! What’s going on? Shouldn’t these ending values be the same, don’t you end on the same note?

Simply put, using Pythagoras’ musical scale you will not end up at C exactly 7 octaves away, but a note whose frequency is 1.74 larger! And this can be noticeable to the listener. The answer to this quandary is simple. Perfect fifths are odd numbered (3/2) ratios as are perfect fourths (4/3). Octaves are computed as even numbered ratios (2/1). Odd numbers never equal even numbers. Therefore, perfect fifths and fourths can never fit evenly within an octave. Hence the utility of the hemitones mentioned earlier. The difference between 129.74 and 128 is known as Pythagoras’ Comma with a value of 1.74.

But you might ask ‘so what?’ Well, first of all, remember at the beginning I asked why there are keys on the piano that have different names but produce the same tone. In Pythagoras’ scale a C# and a D-flat can produce somewhat different tones since their frequencies are different depending on whether you ascend or descend the scale. This is a fact you’ll have to accept unless you read on to see why.

Look above at the clock of fifths and find the F#. If you go clockwise round the clock it is at the 6th hour, 6 perfect fifths. If the frequency of the starting C is 262 then 6 perfect fifths is (3/2)^6 and the frequency of F# is 2984.18. If we go counter clockwise to the F# we start at C with a frequency of 262*(2)^7 or 33536. Then going counter clockwise down the scale 6 perfect fifths (2/3)^6 we arrive at an F# of 2944.46. A mis-match due to the Pythagoras’ comma. The note will have a different tone going up the scale than going down. Thus, the need for two different names because in reality they are two different notes. As an aside, organs were constructed during the late Middle Ages and early Renaissance that actually had two different notes on the keyboard to accommodate this mismatch. Can you imagine the poor organist attempting to play such an instrument?

This mismatch has further serious ramifications. Most composers like to change keys in their songs. It gives interest and a somewhat different mood to the piece. Going from one key to another during the course of a composition is called ‘modulation.’

Here is an example of a modulation in a prelude by Chopin, his Prelude in A-flat major. Listen for the modulation, he changes from flats to sharps giving a different ‘feel’ suddenly to the piece. Can you hear it? Listen below. Such a key change would not have been possible with Pythagoras scale.

In the next sound clip listen to the difference between a minor scale and major scale. The A-minor scale is followed by the A major scale. Then the A-minor tonic chord, the A-major tonic chord, and finally the A-minor again. Hear the difference? In the diatonic A-major scale there is a half-step between the third and fourth notes, C# D, and again between ,the seventh and eighth notes, G# and A. All the other intervals are whole steps. To make it a minor scale, the half-step is placed between the second and third notes B C, followed by D E F# then again the half-step between G# A. A-major has three sharps: D# F# and G#. The A-minor has only the one, G#. I include this little ear training section to help you hear the modulations by Chopin in his Waltz in A-minor. In this simple little Waltz Chopin changes the mood by slipping between A-minor and A-major. Listen and see if you can tell when this happens. First, the scales major and minor and the minor and major tonic chords.

Now, the little Chopin waltz. Incidentally, Chopin Waltzes were abstractions and not really meant for dancing.

Chopin always sounds a little melancholy but did you hear the piece brighten up in the second half of the little clip? He went from A-minor to A-major. Not a huge change but enough to slightly change the mood. Mozart wrote his masterpieces during the period in music known as the ‘Classical Period.” Music composed during this time, the latter half of the 18th century, was mainly for the rich and titled of society and these pampered folks served as patrons to serious music composers such as Mozart. To assure their satisfaction and happiness, Mozart wrote almost all of his compositions in major keys, only rarely using the minor key. He feared the minor keys would depress his rich patrons because of the moody affect engendered by them! It wasn’t until Beethoven a few decades later that minor keys came to be used.

Listen to a short section of Mozart’s piano concerto # 20 in D minor

Did you feel depressed after hearing Mozart in a minor key? I didn’t think so.

Modulation limitations and why they occur with Pythagorean Tuning

Using Pythagoras’ musical scale, modulation between most keys sounds awful. Here’s why. Say, the piece starts out in the key of C major. The composer wants to modulate to the key of E-flat. Then, the E-flat scale should consist of notes a perfect fifth from their preceding note beginning at E-flat: B-flat, F, C, G, D. (Consult the clock of fifths if you are confused here). But now we run into a problem. The perfect fifth of D is wider than A-flat, really more like A natural. But in the diatonic E-flat major there is only a half step interval between the third and fourth note, i.e., G to A-flat. What’s going on?

Remember, preceding round the clock of fifths, consisting of 7 full octaves, you end with a note whose frequency is slightly greater than what it should be. The value of this overshoot is called the “Pythagorean Comma.” How much do you overshoot? Well, for example, if the beginning tonic frequency is say 100, then the final frequency 7 octaves higher should be 12800. But in fact that frequency turns out to be 12974.63. The ratio of these two is 101.3643. This frequency difference would be perceptible to the average listener.

The importance of the Pythagorean Comma is that the simple clock of fifths never completes the circle. Rather than a circle, it is best represented as a never ending spiral that keeps generating new notes of different frequencies, all a perfect fifth apart! This is happening here before your eyes if we start the scale with the tonic of E-flat. Check out the Clock of Fifths: start at E-flat and you see the perfect fifth of D is really A natural. So, modulating from C major to E-flat major will sound out of tune for any melody note or chord utilizing that recalcitrant A. This is because the scale will demand an A natural but your instrument only has available the A-flat. That A is important in the key of E-flat major since it is the fourth note and critical for the popular chord progressions using that fourth or sub-dominant chord.

A brief mathematical description follows, if not interested skip the mathematics without consequence

The simple reason for the Pythagorean Comma is found in the failure of this equality:

(1.5)^12 can not equal 2^7

Odd numbers as represented by perfect fifths and even numbers represented by octaves can never be equal. As we will see, if this fact were known earlier, it would have avoided much fruitless effort.

So, the point is this; in Pythagorean Tuning when you modulate from one key to another, new notes will be produced that sound out of tune. The musician would literally need to stop and retune their instrument! Even without modulating some of the intervals in Pythagoras’ scale sound bad anyway. One in particular is termed the ‘Wolfe Interval’ sounding like a howling wolf it was said. Modulation was possible if the keys were fairly closely matched and the out-of-tune intervals were simply omitted as much as possible. Interestingly, if the musician is playing a musical instrument that is analog such as a violin or trombone or especially the human voice the notes are not pre-estabilished, their ear will ‘automatically’ compensate and hear the ‘correct’ note and fine tune their playing or singing accordingly. On an instrument such as a piano or guitar where the notes are ‘fixed’ and discrete, this fine-tuning on the spot is impossible.

Flatten The Third to Correct The Pythagorean Comma
The interval known as a third is made up of two notes exactly two Pythagorean whole steps apart such between middle C and the E . Given an interval of a perfect fifth, spanning frequencies in the ratio of 3 to 2, the third sounded wider than the discerning musical ears of the early Greeks appreciated. Thus, began numerous attempt to tweak Pythagoras’ scale.

Just Intonation

 During the Renaissance period composers developed increasingly more complex chord progressions adopting thirds and sixths and featured more frequent modulations.  Both of these developments were hindered by the limitations of the Pythagorean scale. In 1558 Giuseppe Zarlino choirmaster at St. Mark’s Cathedral in Venice, developed a new scale termed Just Intonation.  The term ‘just’ refers to intervals between tones that are pure fifths or fourths.

Zarlino tried to minimize the Pythagorean comma and improve the sound of the offending thirds by reducing their ratio from 81/64 to 5/4. He also reduced slightly the interval of the major sixth from 27/16 to 5/3. The step between D and E got reduced from 9/8 to 10/9 as well as that between G and A. He kept the step between A and B at 9/8 and this increased the hemitone step between B and C to 16/15. The difference between intervals C and D vs D and E is rather large; 1.0125 to be exact and this has been called the syntonic comma.

Within any given key the musical intervals of Zarlino’ scale is generally reported to sound better that Pythagoras’. Mostly due to the narrower third. But his scale fares far worse under modulation. Let’s modulate again from C major to G major. Because of the way Zarlino rescaled the interval sizes of some of the notes, most notably between G and A, modulation sounds very out of tune. The original B, now in G major, becomes the recalcitrant F# but further, the perfect fifth of D becomes a new note, sort of A but differing by a syntonic comma from the original A! The reason is that under Zarlino’s tinkering, the original C major scale before modulation featured a narrower minor interval of 10/9 not a whole tone interval of 9/8 between G and A. But this interval must function as a major whole tone after modulation. But unfortunately the die is cast – the strings have been tuned! Of course, the perfect fifth of this new higher frequency A also will be a new note and the spiraling never ends.

Instruments were actually constructed that added keys to accommodate these new notes produced after modulation. It is recorded that Handel actually played an organ with 31-notes per octave!

So many keys are needed because modulations using Just intonation generates more extra new notes than Pythagoras tuning. To make matters actually worse, these new notes were too sharp if the modulation went to a key above the previous key and too flat if modulation went to a key below the previous key. So, modulations sound worse with Just Intonation tuning than they did with Pythagoras tuning. Poor Zarlino’s system of tuning made things worse.

Herman von Helmholtz studied violinists and singers make the proper adjustments during modulations. He concluded that they get pulled into the tonality of the new key and away from the previous one. If they are modulating from C major to G major their tonal “center” shifts and becomes G; no longer C. Their ear “hears” that the dominant perfect fifth of G major must contain the proper F#. The human ear seems to learn what is necessary in resolving the dominant fifth to the tonic not chord.

Mean Tone Scale

 Francesco Salinas (1530 – 1590)a blind Spanish musician, proposed what has come to be known as the mean-tone scale of tuning. The basis for the modifications he made can get rather complex. Some of these concepts I’ll explain later in the blog as they are important and will give you some interesting insights into what makes music pleasant and also unpleasant.

To understand why the tweaks made by Salinas to Pythagoras’ scale didn’t solve anything I need to introduce you to ‘beats.’ Beats occur when two musical notes with, usually, similar frequencies occur simultaneously but are slightly out of sync as illustrated below in the simple diagram.

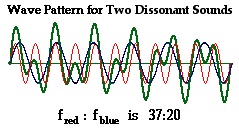
The diagram (taken from musicphysics.com) shows two waves, red and blue, playing simultaneously; overlapping and interfering with each other. One has a frequency wavelength of 370 Hertz and the other 200, i.e., the tone of the red line sounds higher. Displacement from the horizontal line indicates loudness. The sound produced by these two overlapping tones results from combining algebraically the red and blue lines. These together produce the thick green line.

Above the horizontal middle green line the values are plus and below negative. Notice, that this resulting synthetic sound is irregular and varies in loudness as a result of the algebraic summation of the red and blue tones at any point in time. The two notes can either subtract from each other resulting in a softening tone or add together producing a louder one. Further, the synthetic sound is silent when the red and blue tones cancel each other out. This resulting uneven pattern can be very displeasing to the ear. An intermittent ‘beating’ sound is perceptible under these conditions. Herman Helmholtz termed these sound effects ‘beats.’ When two tones produce these beats the experience is termed ‘dissonant.’ Dissonance is most often experienced when the frequencies of the two original tones are rather close together. As we will see , overtones or harmonics may contribute to beating.

Below, I have interposed a tone of 600 Hertz with one of 620 Hertz at the same intensity. It produces a very annoying high pitched whining sound over the combined tones and if slowed down would sound more intermittent like beating. See what you think.

Back to Salinas and mean tone tuning. The third, say a C played with the E above, sounded dissonant using Pythagoras’ tuning. Why? Were the listeners of Salinas’ day just fussy and imagined it? Well, maybe not.

If, say the C is played, its fifth harmonic sounds with five times the frequency of the fundamental C. Remember overtones/harmonics are produced automatically by the fundamental frequency of a musical tone. But in Pythagoras tuning the nearest note to this 5th harmonic of C is E two octaves up. This is often written E” and has a frequency 5.06 times that of the fundamental frequency of C. It would be about a semitone out of tune with the fifth harmonic of C.

If at the same time we sound the E of the Pythagorean third we hear a discordance between the fifth harmonic of C. The former 5 times the fundamental of C and the latter 5.06 time that frequency. A situation ripe for the unpleasant beating as described above. Salinas’ mean tone scale was an attempt to solve for this unpleasantness. The next paragraph describes Salinas’ procedure. It is somewhat mathematical. See if you can work it out. if not just skip to the next paragraph and you’re OK. Basically, Salinas narrows each of the 4 perfect fifths of Pythagoras scale while also narrowing the third just enough to reduce the dissonance between the third and the fifth harmonic of C.

Salinas’ solution was to take each of the four perfect fifths: C – G; G – D; D – A; and A – E and diminished them by an amount so as to give the exact frequency ratio 5.00 to the interval C to E. Mathematically, this turns out to be the fourth root of 5 or 1.49527 replacing the ratio 1.5 of the perfect fifth. Sticking with the mathematics for just a moment, Salinas replaced the two intervals making up the third of Zarlino’s Just Intonation scale of 9/8 and 10/9 with their geometric mean giving a whole tone interval of the 1/2 root of 5.

Unfortunately, these corrections of Salinas did not solve the problem. The foreshortened fifth of 1.49527 was in error of a perfect fifth of 1.5 by 3.15 per 1000. If a clock of perfect fifths was constructed using Salinas’ foreshortened fifths, the clock face had hours going clockwise: C D A E B F# C# G# E-flat B-flat F and C’. Unfortunately, this arrangement produced intervals that often sounded horrific such as that between G# and E-flat termed quite-de-loup or the ‘wolf fifth’ because it sounded like a screaming wolf. In addition, as with Zarlino’s Just Intonation new notes were produced during modulations.

Organs built during the heyday of the mean-tone scale often added many alternative notes to try and avoid these howling intervals. This is why there are notes today on the piano that are labeled C#/D-flat, D#/E-flat, etc. In those days they were actually two different notes.

Nobody is Perfect

As an aside, Sir Isaac Newton, who’s mathematical model of the then known universe, one of human-kind’s brilliant accomplishments, spent a great deal of time trying to determine the best ratios for musical intervals. He was struck by the coincidence of seven colors in the color spectrum and seven notes in the diatonic musical scale. His seven colors corresponded to the notes: red = D, orange = E, yellow = F, green = G, blue = A, indigo = B, and violet = C.

Newton observed that the thickness of the air space between two lenses as he produced red and violet was in a two to one ratio! Believing in the metaphysical connection between color and musical sounds it seemed no coincidence that this ratio corresponded to the musical octave.

Unfortunately, red to violet doesn’t really conform to a musical scale. The 2 to 1 ratio actually includes D to high D, eight notes! Newton fudged a bit to include deep red and deep violet to round out the eight note octave.

Things got worse, his ratio was not 2 to 1 but 14 to 9. Undaunted, Newton concludes that colors and tones were related as the cube root of their squares. That is: ((2/1)^2)^1/3 = (4/1)^1/3 = 1.587 which is close to 1.555 which is 14/9! While his musical scale was promoted by the likes of Voltaire it sadly soon became discredited. It has been said that Newton neither played a musical instrument nor was he particularly moved by music!

OK, let me summarize what I’ve covered so far. At the time of Pythagoras, circa 500 BC, the music was astonishingly simple. No chords and indeed almost no blending of different instruments and or voices. The only intervals between notes were octaves, perfect fifths and fourths. Musical instruments though have been unearthed as far back as ten thousand years ago and were configured to play a pentatonic scale. Such findings strongly suggest caution when we assume that all early music was primitive and simplistic.

A philosopher, mathematician and teacher ,Pythagoras provided the western world with a musical scale that allowed for musical compositions of far greater interest and complexity. His passion for ratios goaded him to discover many scientific principles regarding music. Small simple ratios he reasoned would resonate positively with humans. Pythagoras supported his beliefs utilizing a monochord that allowed him to vary the length of a musical string. Sure enough, consonant sounds arose from the string, if its lengths varied in small simple ratios. At 2 to 1 ratio the string produced the octave. A 3 to 2 ratio produced the harmonious perfect fifth. And the 4 to 3 ratio produced the perfect fourth. He constructed his scale based on these three intervals in the best possible arrangement.

His musical scale advanced western music until far into the Renaissance. But Pythagoras tuning contained a fatal flaw. Perfect fourth and fifths were based on odd numbered ratios while the octave was based on even numbers. Odd can never equal even; Fourths and fifths cannot evenly ‘fit’ into an octave. The overflow is termed ‘Pythagoras’ Comma. This is a serious problem in tuning.

Renaissance composers were utilizing key modulations within a composition. But following modulation a musical scale built of perfect fourths and fifths generated notes that were not tuned in the original key. For example, in Pythagoras tuning the key of C major has no exact F#. If the composition modulated to G major an F# is crucial but alas, no such note is available. Therefore, any chords requiring an F# in the key of G major goes unfulfilled and any substitute note sounds ‘out-of-tune.’ The new notes arose because intervals for perfect fifths widened slightly because of Pythagoras’ Comma. The perfect fifth of B in Pythagoras tuning is F# but it does not lie symmetrically between F and G. The interval between F and F# is greater than that between F# and G. Going round the clock the widening is compounding note after note: the perfect fifth of the F# is C# which suffers the same fate as its predicdsesor.

Many attempts were made to correct Pythagoras tuning. Alas, no solution was possible. Tweaking Pythagoras scale left unsolved the mathematical dilemma that musical intervals based on fifths and fourths were of odd numbered ratios while the octave was of an even number. The result was Pythagoras Comma and the unwanted creation of new notes after modulation.

A New Beginning

Intellectual history is replete with various unexpected leaps of insight and innovation. It dawned on Vincenso Galilei, the father of one Galileo Galilei, that mere tweaks to Pythagoras was insufficient . He proposed in Dialogo della musics antic e minder (1581) a scale where the intervals of all semitones were equal. Each having a frequency ratio of 18/17. The point was that 12 of these (18/17)^12 = 1.9855. This is about equal to 2 which is an octave. Also, seven such semitones (18/17)^7 I = 1.4919 is very close to a perfect fifth of 3/2. Though this would produce octaves and fifths that would sound a bit flat, the Pythagoras Comma would be eliminated. in fact, an interval ratio of 1.9855 vs. 2/1 is imperceptible.

The next step came from Simon Stevin (1548- 1620) who proposed making each semitone (2)^1/12 = 2, exactly the octave. Also, (2)^7/12 = 1.4983 which is also imperceptible from 3/2 – the perfect fifth.

The Coup de Grace – 12 TET = “The Twelve Tone Equal Temperament Scale”

The modern musical scale used pretty much universally today is termed the Equal Temperament Scale. This scale distributes Pythagoras’ Comma equally over the twelve intervals of the scale. Recall here, the twelve hour face for the clock of fifths I told you about earlier. Or think of the twelve keys on the piano from middle C to C” an octave higher. Be sure to include the 5 little black keys. All 12 intervals between notes of the scale are made equal. Below I tell you how this is done. It requires some math and you may wish to skip over the section if you’d rather. The point is all 12 intervals are equal, Pythagoras’ Comma is eliminated, and modulation to any key is possible. Moreover, all intervals sound consonant, no howling wolves and no new notes are produced! To accomplish the equal temperament scale all thirds and fifths must be flattened just slightly. In fact, all intervals are just so slightly out of tune. Pythagoras would not be happy!

How It Was Done

The twelve ‘hours’ round the face of the clock of fifths represents exactly seven octaves. The frequency ratio of the last and highest note, a C, to the lowest and first note also a C is 128F to 1F. Let F, the fundamental frequency of the lowest C equal 1. Then the ratio for the interval highest to lowest C on the clock is 128 to 1. i.e., (2)^7 over 1. If we take the twelfth root of 128 we are essentially dividing up the ratio for the clock into 12 equal parts. The ‘parts’ in this case are the fifths now narrowed to 1.4983 , i.e., the twelfth root of 128 = 1.4983 instead of 1.5. Then all 12 semitones are equal, i.e., have the same frequency ratio of 1.05946: the 12th root of 2 = 1.05946.

The equal temperament scale , 12-TET, had to await the mathematics of extracting roots and a facility with irrational numbers. It was the French monk, mathematician Marin Mersenne(1588-1648) who was one of the first to work out the mathematics for the 12-TET in his Harmonie Universelle 1636. However, it took a surprisingly long time for its universal adoption. There are early examples where it seems most likely that it was employed. The English composer John Bull in the late 16th century composed songs that modulated to keys far away from C major that must have used 12-TET. It was only until the late 19th century that 12-TET became the gold standard it is today.

If you are knowledgable in the history of music or perhaps have taken piano lesson you might be wondering if J. S. Bach utilized 12-TET in his famous composition Well Tempered Clavier 1722 and 1738-44. In that piece Bach presents 24 preludes and their corresponding fugues each pair totaling 24 different major and minor keys.

J. S Bach

I can scarcely write about J. S. Bach without carving out some space to present a little background of this paragon of western composition. And indeed, my stated goal for this blog is to provide you with information to expand your interest and knowledge in music. So, please indulge me and I think you’ll find the following quite interesting.

J. S. Bach (1685 – 1750) was arguably the most influential composer of modern Western music.  Though he wrote in the style of late Baroque music characterized by its contrapuntal structure, Bach’s influence on later composers  was incalculable.   Bach’s work was forgotten after he died 1750 until Felix Mendelssohn in 1829 revived Bach’s St. Mathews Passion. Following its discovery, Bach soon became the standard for musical composition.  His imaginative use of chord progressions and innovative and extensive repertoire, including both sacred and secular music, has inspired composition for centuries extending into American jazz.

Bach lived in Germany when composers worked for wealthy patrons and churches, composing musics for their enjoyment and for religious services. They received little in the way of compensation.  Public concerts were unknown. Composers supplemented their income giving music lessons to wealthy students.  Bach, in his capacity as organist, conductor, and composer of music for various churches, produced a musical output of prodigious proportions.  He was constantly preparing for musical occasions to meet weekly deadlines.   His sacred musical repertoire included masterpieces such as “the Christmas Oratorio” and the aforementioned “Saint Mathews Passion.”

Bach was widely known as a brilliant keyboard player and sought after organist.  He was married twice with 22 children.  Four of his sons became famous composers in their own right: Wilhelm Friedemann Bach; Carl Philipp Emanuel Bach; Johann Christoph Friedrich Bach; and Johann Christian Bach.  C P. E. Bach flourished after moving to England following in the footsteps of another famous German composer George Frederick Handel.  All of Bach’s sons abandoned the late Baroque style of their father, and ushered in a newer style termed classical.  

In 1722 Bach composed a set of 24 pairs of preludes and fugues designed for the keyboard called The Well Tempered Claver.  Each of these pieces was composed in  one of the possible 24 major and minor keys.  He wrote a second set 20 years later while in Leipzig.  In his first set, he did something extremely unusual.  He paired a prelude in the key of E-flat minor (6 flats) with a fugue written in D# minor (6 sharps).  This is  remarkable because it pairs keys that in the past would be enharmonic and require retuning the instrument.  

I’ve presented below. snippets of the prelude in E-flat minor played by Andras Schiff and the fugue in D# minor played by Glenn Gould They of course are played in modern 12-TET and going from E-flat minor to D# minor is a breeze. I hope you are inspired by these little teases of the Well Tempered Clavier to listen to them all. I will spend some time later explaining what a fugue is since I bet you don’t know what it is. Incidentally, Schiff and Gould are two of the finest pianists I could have chosen. Gould a Bach specialist died all too young, now over 40 years ago. Schiff is still with us and playing beautifully.

Why compose two pieces clearly meant to be played back-to-back in two keys most likely to sound bad without retuning? It suggests that the particular tuning employed by Bach allowed for successful modulations between keys! Moreover, whatever the tuning procedure, it maintained the unique character of the particular key in which the piece was written; otherwise why change keys? Composers today do change keys but it is usually because of convenience to accommodate different vocal styles and ranges not because of a difference in quality between keys. The drawback to 12-TET is that while the listener can detect when there is a modulation to another key, the ‘character’ or unique sound of the different key is lost. In earlier tunings, despite their drawbacks, each key had its unique sound. Despite what people might say, different keys are indistinguishable except for those rare individuals with perfect pitch.

These pieces by Bach for the clavier, ( clavier refers to almost any keyboard instrument but particularly the harpsichord),  have been a source of controversy.   It is assumed that the inspiration for these pieces was a system of tuning that allowed all twenty four preludes and fugues to be played in all their various keys harmoniously and without stopping to retune.  It should be noted that Bach was not the first to write suites of musical pieces in several different keys.
Scholars write that Bach was a stickler when it came to tuning.  He even

included tuning in his music lessons.   At the time Bach wrote his first set of preludes and fugues for the clavier, the mathematics necessary for so-called modern tuning were not well known, and probably not to Bach.  
So, are there any clues as to the tuning he did use?  One tantalizing, mysterious clue is a series of squiggles he, or someone, penned on the original manuscript.

 See the top of the picture.  Retrieved from https://www.stefanogreco.com/en/bach-the-well-tempered-clavier.

Supposedly the open curves and curves with extra swirls indicate how fifths and thirds were to be tuned.  The deciphering of this musical Rosetta Stone has been attempted by many scholars.  Intriguing teases include that there are 12 curves – an octave? – the number of open circles perhaps equals the number of fifths in a scale, etc.  It might not have been out of character for Bach to have drawn these squiggles as a sort of puzzle.  He was suspected of adding all sorts of hidden, puzzle-like, figures of notes within his compositions.  The letters of the notes supposedly referred to things beyond the music itself, things of a mysterious and mystical nature.  But other than spelling out his name BACH in notes within his compositions  the rest is mere speculation.

Much like Pythagoras, the historical figure J.S. Bach is shrouded in mystery.  He has his biographers, even sketchy reminiscences by his most famous son, Carl Phillip Emanuel, but they  provide unsatisfying detail about Johann Sebastian the person.  Other than his copious musical output and a few academic notes, Bach wrote nothing about himself.  Add to this, the  complicated nature of Bach’s compositions with multiple melodies swirling around in counterpoint following esoteric rules.  No wonder people conger up speculations about metaphysical truths within his compositions.

 Unfortunately , despite centuries of scholarship on the tantalizing mystery of Bach’s squiggles, there is no universally accepted solution to the riddle.  Even C. P E. Bach with his memoirs about his father sheds no definitive answer to exactly how Bach tuned his Harpsichord for the pieces of the Well Tempered Clavier.

OK, did Bach use 12-TET for his WTC? It is almost certain that he didn’t. The modern equal tempered scale now used virtually world-wide was slow to be accepted. And as I mentioned it wasn’t until the 20th century that it slowly began to be adopted.

Passing Notes on 12-TET

Because of the way 12-TET is constructed any tone can serve as a temporary tonal/harmonic center.  With previous scales this was not possible.  The composer was locked into whatever key was chosen as the tonal center for the duration of the piece.  If a new harmonic center note was chosen, as during modulation, the spacing of notes on the previous scale disallowed a one-to-one matching of notes of the new scale.   With 12-TET any note in the scale can be elevated to that role because mathematically all of the scale tones are spaced at equal intervals; all tones are spaced in multiples of the logarithmic increment between adjacent tones – .08333, (the log of the 12th root of 2). More about logarithms and how we actually perceive pitch later.

Music Before Pythagoras

Pythagoras certainly wasn’t the first person to work through scales and music theory. But, thanks to the chronicling by his many followers, his was the first to be written down. The octave and the appeal of the perfect fourth and fifth certainly must have been known to those who predated Pythagoras. Instruments unearthed by archeologists were more sophisticated than expected. Some of them seemed capable of more complex musical structure than was played at the time of Pythagoras. Lyres were strung to sound the four notes that would form the octave and the perfect fourth and fifth: in the key of C these would be C F G and the C an octave higher.

But certainly musicians must have tired using only these four notes. The intervals or the notes played together that sounded acceptable were limited. The C could be played with the C an octave higher or with either the F or G. But the F and G could not sound consonant played together. But surely musicians discovered the perfect fifth of G and added a D to their repertoire. And certainly one would imagine that they might have preceded Pythagoras in the discovery of what we have been calling the clock of fifths. At some point the discovery certainly must have been made that after a while no new notes could be discovered and essentially if they ended up repeating themselves, going in circles round the clock!

It became then a matter of taste and convenience as to how many notes each culture settled on. But the remarkable thing is how similar the multitude of cultures through out history arrived at such similar criteria. There is variation and several outliers but for the most part everyone throughout history seems to have arrived at remarkably similar musical scales. On average the size of musical scales rarely exceeds 12 notes or falls below 4 or 5. It is even more remarkable that virtually every culture thus far studied has adopted the octave structure described earlier in regards to Pythagoras. I’m getting far afield here but to my knowledge the exceptions are found in the music of various Middle Eastern and Indian music. The famous Indian sitarist Ravi Shankar displayed remarkable virtuosity on his instrument playing note intervals much smaller that the Western semitone and scales much larger than the 12-TET. Some Middle Eastern music even ventures into music that sounds atonal though I’ve not examined these scores.

Ode to All Tuner

I’ve written about tuning as essential to the invention of musical scales but what about the actual process itself? Today, even I have little gadgets that ‘listen’ and tell me everything I need to know about a tone. But what about the poor soul who had to tune Franz Liszt’ piano in 1845 or even more astounding the earlier tuners responsible for tuning the giant organs in the Renaissance cathedrals throughout Europe?! Some of the organ pipes reaching 30 feet or more in length!

Prior to 12-TET, tuning was an idiosyncratic art! Let’s review some basic facts. First, musical tones result from a source vibrating with a primary frequency in the form of a sine wave and generating harmonics or overtones – within the vicinity of an ear. Second, astonishingly, not until the 20th century was a standardized tone adopted from which to begin tuning. The mathematics that I’ve presented above related to tuning were unknown to most tuners. Finally, for the most part we can assume that tuners worth their strips were familiar with whatever musical scale was popular at the time and with the basis principles discovered by Pythagoras.

Given the limitations I’ve mentioned, how was tuning even possible and how could different instrumentalists with different tuners ever play together and sound harmonious? We know that vibrations produce musical tones. But we may not know that it doesn’t matter what the source is for those vibrations. If a saw vibrates at 261.65 Hertz in roughly a sine wave, it will sound as middle C! It may not sound quite as nice as a vibrating violin or guitar string but will indeed sound as middle C.

So, the tuner must start with some standard tone from which all other tones will be related. The, mostly, universal standard today is the A above middle C with a frequency of 440 Hertz. But before around 1840 the tuner just chose the standard arbitrarily! Think of the chaos if musicians came from different towns to play together. Cacophony rained! Everyone is tuned to a different standard.

So, the tuner chooses a standard then what? Let’s say he uses Pythagoras’ tuning. It seems unclear that vibration was understood enough to actually be of much help to the tuner prior to the pioneering work of Fourier on vibration/wave analysis. Thus, prior to the 18th century vibration analysis was little known. Even the unit of a second wasn’t developed before the 16th century.

Tuning forks were invented in 1711 (John Shore) so no help there. Pythagoras, or probably his disciples, left behind his rules relating musical string length to pitch which would suffice in tuning small stringed instruments. But if strings were especially long, length became only one of several parameters used to determine their pitch. Thickness and tension also came into play. Think about a concert grand piano. Some of the lower strings would need to be longer than the length of a stage to be tuned properly. So if you examine a piano string at the bass end you’ll see it is wrapped on the outside by a smaller diameter string to thicken it. And it is under serious pressure. Some bass strings are under 160 to 200 pounds of pressure and the total pressure of the piano can be 3500 pounds. Yes, in the old days pianos would indeed implode on stage during a concert!

The amazing fact of tuners is that just a couple centuries ago they tuned by ear alone once they established their standard pitch! Just think of that! Tuning a giant organ with hundreds of pipes 20 to 30 feet or more in length just by listening. The length of pipes was adjusted during tuning. Most pipes had built in inserts than could be pulled up or down. But it turns out after much training, that humans have the ability to detect when a string or pipe, etc is out of tune and bring it into its proper relationship with the other pitches all related to the standard pitch chosen by the tuner.

The source for vibration in a pipe organ is of two types. Columns of air divide into two streams upon encountering an obstacle inside the pipes. Once divided the two streams form alternating whirlwind eddies. Like a stream of water hitting a rock divides as it passes the rock. These formations alternate in regular intervals functioning as vibrations like those of musical strings. See the figure below of eddies of air forming on each side of an obstacle inside an organ pipe.

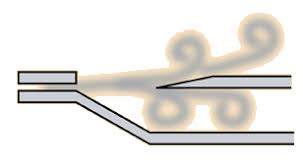
Pitch is determined by the frequency of alternating formations of the wind eddies per second. This of course is directly correlated to the wind speed of the column of air. A whirlwind is formed every time the wind passes over a distant equal to 5 2/5 times the diameter of the obstacle. This makes it possible to calculate the pitch of the musical note formed. Suppose wind is flowing 704 inches per second over a half inch obstacle. Air passes over the 1/2 inch diameter of the obstacle 1408 times per second. Divide this by 5 2/5 and we obtain 261 – exactly middle C! Pitch of this wind whistle phenomena is directly proportional to velocity of the air column. This process for producing music is accomplished in the ‘flue organ pipes.’ A second type of organ pipe has a wooden reed that vibrates. The sound pressure waves are modified by the length and diameter of the particular pipe. Longer pipes produced lower pitches and shorter ones, higher. Also, the material used to make the pipe affects the quality of the sound.

If you play the guitar, banjo or violin, or some other small stringed instrument, you may have trained yourself to tune your own instrument. Most professional musicians do tune their own instruments. The exception being pianists and certainly organists. Also, if you play a wind instruments that produce vibration from the musician’s lips, e.g., the trumpet, trombone or flute the tuning starts with the player! Instruments with reeds, e.g., clarinet or oboe etc. would not allow much modification in their pitch aside from replacing the reed.

Today, we have electronic devices that seem to practically do the work for you. I admit I don’t tune my guitars without a little tuner that tells me when I’ve hit the correct frequency. Most electronic keyboards really never need tuning, it is all hard wired. Of course if the electricity goes out well then…..

A piano tuner begins by tuning the standard, usually A at 440 Hertz. In earlier centuries middle C was used as a standard, at about 262 Hertz. Of course the tuner had to have some way to produce that standard pitch. I suppose some tuners may have possessed perfect pitch. Then the octave note, usually lower, is next tuned. The tuner plays the middle C then the lower C and listens to hear any ‘beats.’ Beats were discussed earlier. They occur when the frequencies from the two notes slightly interfere with each other, i.e., they are not in sync. If beats are detected the octave is not quite ‘in tune’ and the string is loosened or tightened by a wrench until the beating disappears. Remember, middle C and C an octave lower should have identical sine waves only with one twice the Hertz value (cycles per second) as the other. They should map perfectly onto each other, only with one having twice as many cycles per second.

The third is usually tuned next in exactly the same way. Then the perfect fifth and fourth. Of course the tuner too is stuck with the Pythagoras Comma unless tuning in 12-TET. The tuner today will come equipped with the latest gadgets. Mainly, they would want a frequency reader that provides the frequency of whatever pitch each note produces. These are simple and reasonable inexpensive. Also handy would be a pocket calculator. But most tuners still listen for beating to guide their tuning.

The tuner of today would start with a standard pitch. Today this standard would be A at 440 Hertz. The 12th root of two would be found to be 1.05946 which serves as a multiplier for finding the exact frequencies of the notes. Later I will explain in more detail the exact function of this multiplier. But for now I will tell you that its multiplicative function results in the tones being spread logarithmically.

The following formula provides the exact Hertz value for each note making up the 12 notes of the 12-TET scale. Though the formula looks formidable it is pretty easy especially with a decent hand calculator.

It says that the frequent of the note we are trying to determine equals the frequency of the reference standard, here 440, multiplied by (a) the factor (1.05946) raised to the number (n) of semitones from the reference note. The formula is given below.

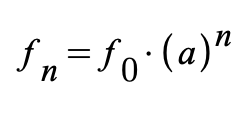
Let’s try it out. I want to get the frequency for the first semitone above the A of 440, i.e., A# so the exponent n will equal 1.

The factor 440 * (1.05946)^1 = 466.1624. Where the n is 1. How about the next one which would be the B natural and the exponent n would be 2. The Hertz value for B natural would be = 493.88. In this way we can obtain all the frequencies or Hertz values, for the 12 notes of the A major scale. The tuner might still tweak things to be sure there was no unpleasant beating to interfere with the new pitch. Our multiplier of 1.05946 is the non-determining decimal obtained by taking the 12th root of 2. Using it as a factor we divide the musical scale into 12 logarithmically spaced intervals. We perceive these intervals as equally spaced.

The formula above provides the correct frequencies but these are not based on true thirds, fourths or fifths. All these will be just slightly out of tune, flattened to be exact. This procedure eliminates the Pythagorean Comma and any key will map one-to-one onto any other key. There are no howling wolf intervals and modulation to any key is possible without sounding out of tune. The price you pay is the slightly out of tune intervals (they are slightly flattened) and each key loses any affective individuality. The key of B-minor does not sound any more soulful than any other key. In general, the musical world has been willing to accept the shortcomings of 12-TET in exchange for its benefits.

In General We Perceive the World Logarithmically

Listen to the following two series of tones. They start at 330 Hertz and increase either by adding 100 Hertz to each successive tone or by multiplying each successive tone by 1.3. The first method produces a linearly increasing Hertz function, the second a logarithmic one. Decide which of the two series of tones, the first or second, is more evenly spaced.

Unfortunately, the range was necessarily rather narrow, but more people would say that the second logarithmic spacing sounds more evenly spaced. The reason is probably anatomically determined by the design of the cochlea in our inner ear. The process of evolution has favor this arrangement as the best design for survival and reproduction.

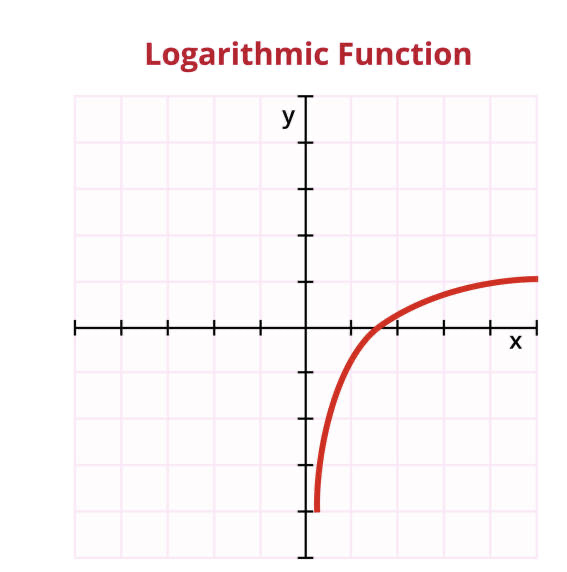
The graph above illustrates a simple logarithmic function. It rises steeply at first then gradually levels off. Let the y-axis stand for our sensitivity to energy level change and the x-axis energy level. We’re most sensitive at low energy levels and least sensitive at high levels. At the left end, the red line moves just slightly along the x-axis to achieve a jump up of one horizontal line on the y-axis. At the right end, the red line must move right three vertical lines along the x axes before ascending one horizontal line. That is, it takes a large energy change for us to detect it when energy level is already high. But when energy level is already low, we can detect small energy changes.

Logarithmic sensitivity turns out to be beneficial.  At lower energy intensities our sensory systems detect very small changes.  Take loudness for example. We need to hear the soft crackling of blades of grass as the beast sneaks up on us.  It may mean the difference between life and death.  But once the beast is near enough to begin running, we have already heard it – or it’s too late. Sensitive detection at already high levels is not so important!  

We are at a quiet indoor theater and  someone whispers to us.  Unable to hear them clearly we cup our ear and it takes just a slightly louder whisper to make things clear.  But at a party where conversation is loud that same person now has to really yell to make us hear what they are saying.  Detection at already higher intensities is not nearly so good.  What was easily detectable at lower intensities at loud intensities it gets lost. This is logarithmic perception.  Linear perception would mean that we perceive the same magnitude of change equally in either a soft or loud environment. 

Our sensitivity to pitch is also logarithmic. The psychological ‘distance’ between middle C and C one octave higher sounds roughly the same as that from the high C to the next higher C and so on. All the octaves seem equally spaced. But this does not mean that the frequency differences among all of these octaves are equal. These are logarithmically spaced. Watch:

Here are three octaves of C showing the frequencies of the lower and upper bounds of the octaves:

261.6 – 523.2

523.2 – 1046.4

1046.4 – 2092.8

The ‘distances’ between these octaves in frequencies are: 261.6; 523.2; and 1046.4. These clearly are not equal, in absolute terms the intervals keep getting wider, but they sound equally spaced. Why? Because they are logarithmically spaced we perceive them as equally spaced. That is the way we perceive pitch as well as most types of energy. Below I go into this a little bit more arithmetically and it is not necessary unless you are interested.

What do I mean by logarithmically spaced? Recall the formula for obtaining frequencies for the 12 semitones of the 12-TET scale.

The new frequency =( reference frequency) x (multiplier)^n . When dealing with octaves the multiplier is 2 and the exponent n is the number of steps from the reference frequency of 261.6.

The first frequency is the same as the reference of 261.6 with n = 0, 2^0 =1. The second frequency will be 261.6 x 2^1= 523.2. The third frequency will be 261.6 x 2^2 = 1046.4. And the fourth frequency will be 261.6 x 2^3 = 2029.8. The definition of a logarithm is the number of times a given number must be multiplied by itself to equal some other number. So, for example,

The 2 must be multiplied by itself 3 times to equal 8 so the logarithm base 2 of 8 equals 3. Here we are multiplying a constant 261.6 by a number multiplied by itself n-times to achieve another number. This process produces a logarithmic series of frequencies we perceive to be equally spaced.

If instead, we added 261.6 to each note we’d arrive at: 261.6, 523.2, 784.8 and 806.4. These frequency numbers are in a linear series yet surprisingly, we would not perceive them as an equally spaced series.

I mentioned that there is an anatomical reason that apparently accounts for our logarithmic perception of pitch. The basilar membrane located deep within the inner ear has hair cells that get stretched by pressure waves from a vibrating source outside the ear. The basilar membrane is frequency sensitive, lower frequencies at one end and higher frequencies at the other. But the membrane seems laid out logarithmically. At the longer wavelengths, lower pitches, there is greater discriminative sensitivity. This sensitivity diminishes as the wavelengths get shorter, higher pithes. Roughly, the different octaves would occupy equal spacing on the membrane though their linear spans would be unequal.

The basilar membrane is not flat as pictured below but curled up much like a snail shell. But laid out flat it resembles the graphic bellow. It contains 16,000 hair cells each sensitive to a particular frequency. The hairs are located along the membrane from shortest to longest. The shorter hairs are sensitive to high frequencies and the longer ones the lower frequencies analogous to the strings on a piano or harp. It has been carefully determined that the sensitivity of the hair cells is logarithmic. Sensitivity for octaves would appear equally spaced along the membrane though we now know the frequencies for the various octaves is logarithmic.

One more example of the logarithmic perception of frequency/pitch.

On the piano, if you move one key to the right, the frequency of the pitch does not increase by a constant amount. On the lowest note of the piano, moving one key to the right increases the frequency by less than 2 Hertz. At the top end of the piano, moving up one key increases the frequency by over 200 Hertz. If you took the logarithms of the frequencies for each note, moving one key up from its neighbor increases the log frequency by a constant amount, about 0.025. It is this change to which we are sensitive.

Musical Cents

This section is not particularly mathematical but as you glance through it unless you find it useful or interesting it may be skipped. There has developed a measuring unit termed ‘cents’ which may help as a reference measuring the ‘distances’ between musical intervals. There are to start with 1200 cents in any one octave. Since there are 12 semitones in the 12-TET, each semitone is given the value of 100 cents. If two tones are 400 cents apart this would define a third. If two tones are 700 cents apart this defines a perfect fifth. And so on.

In psychological experiments designed to measure sensitivity to energy changes, participants are presented a standard tone of a given frequency. Then the energy is slowly increased, with pitch this is frequency. At the point when the participant ‘just notices a difference’ that frequency difference is termed one JND. This procedure is repeated several times and the average just noticeable difference is determined over several trials. It turns out that the JND averaged over many different participants and over many different standard frequencies is 5-cents. But keep in mind that this process is logarithmic.

Here is an example. Look at the semitone A to B-flat, 100 cents, as it moves from the lower ranges to higher ones and notice that the it takes more and more frequency energy to achieve one JND. The numbers following the notes, 0 – 7, indicate the varying octaves low to high on the piano.

A0 is 27.6 Hz and B-flat0 is 29.135 Hz and the frequency increase is 1.635 Hz. This semitone interval would be 100 cents. If a JND is equal to 5 cents, then 0.081 Hz is the amount A0 of 27.5 Hz must be increased to be just noticeably higher in pitch. The B-flat 0 then is well above one JND: 29.135 is well above 27.6 + 0.081 = 27.681.

Now, let’s go higher up the piano from A4 to B-flat4, 440 Hz to 466.16 Hz with a frequency increase of 26.16 Hz. This jump of one semitone is 100 cents. The JND of 5 cents is 1.27 Hz.

Finally, let’s go much higher up the piano from A7 to B-flat7, 3520 Hz to 3729.3 Hz with a frequency increase of 209.3 Hz. For this jump of one semitone at a much higher range, the JND is 10 Hz.

Once again looking at the JNDs as 5 cents, we see the frequency energy added to a standard A must be increased even more to be detected by one JND. Again, illustrating the logarithmic nature of our frequency perception of pitch. It goes from 0.08 to 1.27 to 10 Hz as A goes from 27.5 to 440 to 3520.

Musical Scales Part II: Music Theory Slightly More In Depth

If you’ve stuck with me so far you’ve come along way toward understanding the origins and foundation of musical theory. I’ve gone over the development of the first musical scale, at least in the Western world by Pythagoras. He produced the foundation for musical development for centuries. His musical scale was based on the most consonant musical intervals, the octave, perfect fourth, and perfect fifth. The scale was termed the diatonic and has a particular form. It consists of seven notes; five notes separated by intervals of whole steps in the ratio 9/8 Hertz and two notes separated by smaller intervals that were partial whole steps with Hertz ratios of 256/243. These partial whole step intervals termed hemitones, were necessary to ‘fit’ intervals of perfect fourths and fifths evenly within an octave. Pythagoras constructed his perfect fourths and fifths out of Hertz ratios that were odd numbers (4/3 and 3/2). The Hertz ratio for the octave, however, was even at 2 to 1. Odd numbers don’t equal even numbers. A scale of only fourths and fifths will be slightly larger than an octave. Recall the circle of fifths. This outcome was termed the ‘Pythagoras Comma.’ The ‘hemitrones’ in the diatonic scale they come at intervals 3 and 7.

As I described in the first section of this work, the Pythagoras Comma made changing keys within a musical piece problematic. The key into which the composition modulated contained certain notes with frequencies that were slightly different from those in the original key that often produced dissonance.

The Pythagoras Comma caused problems for musical developers and theorists for centuries and resulted in today’s equal interval scale of 12 notes all spaced one-half step apart.

But the two hemitones were of a mixed blessing. The hemitones of Pythagoras turned out to have a central role in later scale and mode development. The placement of the two smaller intervals can vary within a musical scale. The diatonic scale first established by Pythagoras placed them between the third and fourth notes and between the seventh and eight notes. The eighth note being the note an octave above the tonic. But there is no reason that they must appear only there.

The Development of Other Scales or Modes

The diatonic scale was developed by Pythagoras. It consisted of seven notes logarithmically increasing in frequency such that they sounded equal intervals apart. An eight note, double the frequency of the tonic was added to complete an octave. But the internals between the 3rd and 4th notes and 7th and 8th notes were somewhat less than half that between the other notes. Pythagoras called these hemitones. These were necessary to ‘fit’ all eight notes within an octave.

A C Major scale went: C. D. E. F. G. A. B. C. The ratio between the frequencies values of successive notes was 9/8. The two shorter exceptions came between E and F and B and C. No matter which Diatonic Major scale you choose the placement of these shorter intervals are between the 3rd and 4th notes and the 7th and 8th notes. Take the key of B-flat major: Bb C D. Eb. F. G. A. Bb. The placement of the flats (b) causes the shorter intervals to be placed correctly: between the D and Eb and between the A and Bb. This is the reason for the sharps and flats.

Diatonic Modes change the order of placement of these shorter intervals.

The pattern of intervals for any Diatonic Major scale is:

W W Fr W W W Fr The W = a whole tone and Fr = a smaller fraction of a whole tone.

This pattern holds for all Major diatonic scales. But if you change the location of the Fr intervals you would create modes. Modes are used to add interest and particular moods to compositions. I’ll present some examples at the end of this section. Modes as described below were used often during the Renaissance period. But modes fell out of favor. They became popular again during the early 20th century as composers experimented with new means of expression. Their idea was to break with tradition and give their compositions a fresh sound.

There are seven diatonic modes: Ionian; Dorian; Phrygian; Lydian; Mixolydian; Aeolian; & Locrian. A different mode for each of the seven different diatonic scales. Each mode has a unique interval pattern. The differences are achieved by varying the position of the two fractional intervals. I labeled these Fr above.

We start out with the diatonic interval pattern: W. W. FR. W. W. W. FR. The two smaller intervals occur between 3rd and 4th notes and 7th and upper tonic notes. But they systematically change position for each mode. The two smaller intervals shift ‘downward’ one position for each successive mode. Think of the seven notes plus the upper tonic tone as occupying eight different slots. That is:

Diatonic	W	W	F	W	W	W	F
Ionian	W	W	F	W	W	W	F
Dorian	W	F	W	W	W	F	W
Phrygian	F	W	W	W	F	W	W
Lydian	W	W	W	F	W	W	F
Mixolydian	W	W	F	W	W	F	W
Aeolian	W	F	W	W	F	W	W
Locrian	F	W	W	F	W	W	W

The chart lists mode interval patterns for the standard diatonic Major scale followed by those for the seven diatonic modes. Note that the pattern for the Ionian Mode is identical to that of the diatonic. The cell contents for the Dorian, shift so that the Ws and Frs move left one cell. The content at the leftmost cell shifts to the now empty cell furthest to the right. The pattern for the Phrygian is shifted to the left by one cell again. This systematic shifting of Ws and Fs continues for each of the modes assuring a different pattern of intervals between notes for each mode.

You wouldn’t think shifting the position of the shorter intervals would make a great deal of difference. But it does. I’l play examples to let you see for yourself.

There is another way of determining the interval patterns for the modes. Start with any Major diatonic scale, I’ll use C Major. The Ionian has as its diatonic note the exact diatonic as, C Major – middle C. Therefore, the Ionian mode will have the identical interval pattern as C Major. The Dorian mode will start out on the second note of the C Major scale the D. If you play an instrument or have access to a piano play successive notes up the C Major scale but start at D. Note the pattern of those successive notes. They will follow early those of the Dorian mode as displayed in the charts. There is a whole tone between D and E. The first smaller interval comes between the E and F, the second interval as shown on the charts. Keep playing and the second smaller interval between B and C is now the next to last interval as shown in the charts. Each successive mode will have as its tonic E then F then G and so on . You can then check to see that the intervals patterns you play match those on the charts. Below I’ve illustrated the scheme on the chart.

Ionian	W W Fr W W W Fr
Dorian	W Fr W W W Fr W
Phrygian	Fr W W W Fr W W
Lydian	W W W Fr W W Fr
Mixolydian	W W Fr W W Fr W
Aeolian	W Fr W W Fr W W
Locrian	Fr W W Fr W W W

Ionian Mode	The C Ionian Mode C D E F G A B C
Dorian Mode	The C Dorian Mode C D E-flat F G A B-flat C
Phrygian	The C Phrygian Mode C D-flat E-flat F G A-flat B-flat C
Lydian	The C Lydian Mode C D E F# G A B C
Mixolydian	The C Moxolydian Mode C D D E F G A B-flat C
Aeolian	The C Aeolian Mode C D E-flat F G A-flat B-flat C
Locrian	The C Locrian Mode C D-flat E-flat F G-flat A-flat B-flat C

Listen below to the seven different diatonic modes. The first mode is the Ionian mode and it will sound exactly like the C Major diatonic scale. Following the Ionian mode see if you can hear the differences in the remaining modes. The differences certainly can be heard but you may wonder if they make much different in a song. I’ve provided a snippet of a classical Beatles song to illustrate that it does.

Now, listen to “I Feel Fine” an old song by the Beatles that uses the Mixolydian mode. It is heard immediately in the guitar riff at the beginning by George Harrison. First, have a listen to this classic old song that still sounds good after all these years.

The Beatles had varying degrees of musical training and theoretical knowledge. But it is clear from this song that someone in the group was familiar with diatonic modes. Or who knows, maybe they just fooled around with their guitars and blindly discovered interesting sounds but my guess is that they knew much more than given credit for. In any event let’s analyze that opening riff by Harrison. If you can read the score below it looks at first that the riff played by George Harrison starts off with a G indicating that the tonic is G and therefore, the key must be G Major. However, G Major has the seventh note an F#. In this little riff the F is not sharped, but natural. And throughout the song the F is not sharped giving the melody just the slightest edginess. If you construct a G mixolydian mode you’ll see that the F is not sharped. If fact G mixolydian has no sharps or flats. Listen again to the audio above of ‘the Beatles song ‘I Feel Fine’ and see if you can hear the affect of the natural F on the melody. The same mode is used for another Beatle classic ” Norwegian Wood.” Please excuse all the white space below this next graphic.

The Harrison riff at the start of “I Feel Fine” simplified, is given above. Note the F is not sharped and also note the interesting syncopation. Beatles use syncopation to add interest and surprise to their music. In most pop music today you seldom hear syncopation used in interesting ways if at all. But that F natural, not sharped, precludes the resolution expected by the listener when going from the seventh note to the tonic G. Whenever this progression is used in “I Feel Fine” it produces a strangely odd feeling to the sound.

Parent Major Scale

For every diatonic mode there can be determined a ‘parent’ Major scale. Though this may sound very arbitrary and seemingly useless, knowing the parent Major scale can be of use when improvising music and deciding which keys/scales you’d like to transition to in your playing. You may certainly skip this section if you don’t feel it will benefit you but you may just want to follow along to get the gist.

There are seven diatonic modes, (though more can be created from the 12 tones in the chromatic scale) one for each note in a diatonic scale. I arbitrarily choose the diatonic C Major scale from which to generated the seven modes. I could have used any of the seven diatonic scales, it is the pattern of intervals between the notes that’s important and this pattern is the same for all Major diatonic scales.

To determine the parent diatonic Major scale for each of the diatonic modes lets return to the old reliable circle of fifths. Check out the new and improved version below.

What’s new about this version of the circle of fifths is the addition of the number of sharps or flats each scale has. Begin with C and go round the circle. So, for the scale of G there is one sharp all the way down to F# which has 6 sharps. Going counter-clockwise , the scales are shown having flats. You can think of going counterclockwise as going down the scale and clockwise as up. You sharp a note by going up a half step up. You flat it by going a half step down. So, C to F is gong down and the scale of F has one flat. The dividing point is at 6 o’clock; there is a D-flat and C# scale as well as an F# and G-flat scale. Makes sense because there is no B# scale since B# really becomes C!

Now, once you determine the notes of a diatonic mode count the number of sharps or flats. The parent diatonic scale will have an equal number of sharps or flats as seen on the circle of fifths.

The A Lydian mode has four sharps. Its notes are: A B C# D# E F# G# A. Looking on the circle of fifths we see that diatonic E Major has four sharps and is therefore, the parent scale of A Lydian mode. You can maybe see that this is handy if you are improvising in E Major. It becomes an easy matter to move into the A Lydian mode for a different and interesting sound.

I

HARMONIC MINO

There are yet many other scales or modes that can be derived from the basic diatonic scale with its particular interval pattern. It is a fair point to ask whether it’s necessary to learn about these mode for one to enjoy music. There are many of them for sure, and you can certainly enjoy music of all genres without knowing a lick about these many modes. The question is how much do you want to understand what goes into producing the interesting sounds of many composers/groups? The diatonic scale provides almost infinite possibilities for the composer. But composers during the 20th and 21st centuries wanted different ways to express themselves. One way was to utilize the different sound qualities offered by modes.

We’ve already described in some detail the diatonic modes derived from the Major diatonic scale. Good examples were already mentioned. But just to further my point here’s some more. This is Carlos Santana the incomparable guitarist composer doing one of his classic songs. He utilizes the Dorian mode.

One final example of the use of modes in popular music comes from the musical genius of the 1960’s, Jimi Hendrix. Hendrix was one of the most inventive guitarist’s of his generation. He explored all genres of music and was incomparable as a composer and musician. Unfortunately as with so many rock artists of his time he succumb to drugs at the early age of 27. On this example, he plays “All Along the Watchtower.” His music was full of surprises and it’s hard to say the flavor of the Aeolian Mode is fully experienced here. But listen carefully and you’ll hear chord progressions that aren’t common and suggests that you are not in the diatonic scale. By the way, you’ll notice my examples aren’t from the most current pop music. This is because there are few such examples. More on this later but generally today’s pop music is more about the lyrics and the performance style. Taylor Swift is a talented lyricist, but her music is like so much pop music today where the emphasis is not on experimenting with the music itself.

Here are the Harmonic Minor Modes. These modes are based on the yet another interval pattern structure. It is a reordering of the diatonic structure. The pattern goes like this:

W. Fr W W Fr W Fr If we started on A the scale would be: A. B C. D. E F. G# A. If you have access to a piano when you play this you’ll have a half step between B and C, between E and F and between G# and A. Notice, you have a step and a half between F and G#! This imparts a moody or melancholy sound to the scale and makes it not a diatonic scale. There are seven harmonic minor scales.

Aeolian (#7): the first harmonic minor mode has the same name we used for one of the diatonic modes. And indeed, they have very similar structures except the seventh note is raised half a step in the Aeolian minor mode – hence the #7 following it. The Aeolian #7 has what is termed a major 7th interval between its tonic note and the seventh note of the scale. The Aeolian diatonic mode has a minor 7th interval between the tonic and the seventh note. The Aeolian minor mode, starting on any note has the following interval pattern: W. Fr. W. W. Fr. (W + Fr). Fr. The (W + Fr) indicates the interval is a whole step and a half. Look at the Aeolian beginning of the key of A above to get the pattern in your mind.

Locrian (#6) just as with the diatonic modes, each successive mode has the half or fractional intervals and the step and a half interval shifted down to the left one place. So the Locrian mode has the interval pattern: Fr. W. W. Fr. (W+Fr) Fr W. Starting on A: A B-flat. C. D. E-flat. F#. G A. This is the very rare instance sharps and flats have to be used in a scale. There is a rule in music that alphabetic letters may not be skipped. The Locrian minor mode has a major 6th. Hence, the designation #6. The diatonic Locrian has a minor 6th.

Ionian (#5) You can guess this mode has a major fifth whereas the diatonic Ionian has a minor fifth. This means that that odd step and a half interval will occur between the 4th and 5th notes. The pattern shifts down one place to the left: W. W. Fr (W+Fr). Fr. W Fr. Starting on A: A. B. C#. D. E#. F#. G#. A. Notice that the E# is really the F since we must raise E half a step to achieve a whole step between D and E. Indeed, this can get tedious so try if you can playing the modes on an instrument.

Dorian (#4). W. Fr. (W+Fr). Fr. W. Fr. W. Starting on A: A. B. C. D#. E. F#. G A. See if you can see why this is called the Dorian #4.

Phrygian (#3). Fr. (W+Fr). Fr. W. Fr. W. W. Starting on A: A. B-flat. C#. D. E. F. G A. Again the need to to utilize both sharps and flats.

Lydian (#2). (W+Fr). Fr. W. Fr. W. W. Fr. Starting on A: A. B#. C#. D#. E. F#. G#. A. The B# is really the C when you raise B half a step.

Mixolydian (#1). Sometimes called the super Locrian. Fr. W. Fr. W. W. Fr. (W+Fr). This is really an odd scale in many ways. To make it simpler let’s start this time on C.. C. D-flat. E-flat. F(double flat. really the E) G-flat. A-flat. B(double flat. really the A) C. Wow, crazy! The mixolydian is often called the super Locrian because they have the same notes except…the diatonic Locrian has a ‘perfect 4th’ while the super Locrian has a diminished 4, i.e., the 4th note has a flatted. In the C Mixolydian above the F is a double flat. The same is true of the 7th note: diatonic Locrian starting on C has a minor 7th the super Locrian has a diminished 7th and is double flatted!

Some Examples in Popular Music

After all of the somewhat tedious explanation of the harmonic minor modes it’s time to relax a bit and listen to some of them. Forgive me but I’m going to illustrate the harmonic minor mode using again examples from earlier rock and roll music. The popularity of the Beatles I strongly believe was due in large part to their creative use of Major and minor modes. It gave their songs a new and interesting sound that set them apart from the typical music of the day. Most popular music at the time the Beatles came to the United States was either quite simplistic or based on earlier forms from the 1940s and 1950s. Nothing wrong with that but the time was ripe for a new sound. The Beatles provided it. The use of modes gave their music a rather strange haunting and edgy sound. Listen to a couple of them written in the harmonic minor Aeolian mode. The first is “Long and Winding Road.” The major seventh provides the punch giving this song a unique mood. See what you think.

The second example, again the Beatles, is “Eleanor Rigby.” The song created quite a sensation; somewhat strange yet provoking interest. It also features some interesting rhythms and utilized a broader range of accompanying instruments than found on most popular songs of the day. Who would have guessed a rock and roll group would incorporate a string quartet? Songs like “Elenor Rigby” greatly broadened the audience of the Beatles by its unique appeal. What do you think?

Rhythm

Music has several key components. Everyone agrees that melody is one such key. I emphasized earlier the importance of the musical interval. The sound of at least two notes played one after the other. A single note from say a violin or trumpet may sound pleasant but hardly satisfies as music. It is the juxtaposition of notes one after the other that we associate with a musical melody. It is usually the melody of a musical piece that we recognize first and by which we may judge it.

A musical melody require spacing-in-time; one note follows the other after a given interval of time. Twelve notes spread out over several octaves and spaced over a seemingly endless variety of temporal intervals; there is almost an infinite combination to choose from. No wonder different songs seem endlessly possible.

I want here to address the spacing of notes. How the individual notes are spaced over time is termed rhythm. Rhythm is necessary for music. The sound of a carpenter’s hammering is not sufficient as music. But if the hammering is rhythmical? Well, let’s see.

OK, OK I cheated. That was Steve Gadd a fabulous drummer doing a brilliant drum solo. But you must admit there is no melody and no chords, just a stick hitting a stretched drum head and a symbol thrown in toward the end.

Yes, that was men hammering a stake into the ground. Perhaps not quite like Steve Gadd but getting there. Listen again to three women pounding grain in a small mortise. You have to sort of shut out their voices and listen to the rhythmic pounding. It’s like three quarter time, like a waltz. “One-two-three, one-two-three, one-two-three…” It’s almost musical isn’t it?

I may be stretching the point but rhythm is at the heart of so much music. Why do we dance to certain songs and what about them that makes us want to dance? I submit that rhythmic pounding/drumming and dancing was the first music. Here’s a couple more examples of the use of rhythm.

This next example is Gene Krupa a famous drummer from the swing era of the 1930’s and ’40’s. He played with most of the famous swing bands such as Tommy Dorsey and also had his own band for a while. Here he is on the song “Tiger Rag.”

One final example is Mel Taylor of the Ventures an early 1960s group on their famous hit “Wipe Out.”

Rhythm: Reading A Simple MUSICAL SCORE

I hope didn’t overdo my enthusiasm emphasizing the fundamental importance of rhythm in music. In this section I want to go further into rhythm but to do so I’ll need to introduce basic musical notation often called a score. Many of you may be very familiar with reading Musical scores if you are in a choir or play a musical instrument. But others may not and it may look rather intimidating when you first encounter one. But I will start simple and I think you will find it fun to learn to read what your favorite artist does when they produce music. Below is an our first look at a simple score.

Above is a musical score. Notice the double set of five lines. These are called staffs. The upper with the ampersand is called the ‘treble clef’ and the lower with the backward ‘C’ is the ‘bass clef.’ Notes are written on and between the lines of both treble and bass clefs. But the first thing I want you to notice are the numbers 4 above 4 at the start of the score. These number signify the “time signature” for this particular piece of music. The double set of five lines are divided here into four sections by occasional vertical lines. The sections are called ‘measures’ and are sort of the basics unit for a score. The top number of the time signature tells us the number of ‘beats’ per measure. Here we are told there will be four beats in each of the four measures. So, we would count “one two three four” or tap our toe four times before moving on to the next measure where we would start counting over again. A lot of music has four beats to each measure. I’ll let you listen to some in a moment.

The lower number of the tie signature signifies how the measure will be divided up given the four beats. The bottom 4 can be roughly thought of as a fraction – but only roughly so. Here it tells us that the measure will be divided up into quarters as the fraction 1/4. So, 4 over 4 indicates 4 beats per measure dividing the measure into quarters. But what exactly does this mean, i.e., divided into quarters? Well, here’s where musical notation comes into play.

The notes making up a melody of a song are represented on a score by dots some with little stems on them. The configuration of the dots signify duration, how long the note should sound. That note duration is represented by a fraction of the measure. Music is temporal, the sounds of the notes come and go as time moves on at a constant rate. Think of moving from left to right on the score at some constant speed.

If you want four notes in sequence to sound with the same duration within a measure each one would ‘last’ one quarter of the time it takes moving from left to right within one measure. To accomplish this you could use ‘quarter’ notes that look like filled dots with a stem attached. Look at the first and second measure in the score above. It shows four quarter notes and they are so named because they will sound for one quarter of the time it takes to move at a constant rate from left to right of each measure.

The speed moving left to right within the measures is called the ‘tempo.’ Let’s say you want the tempo to be 4 seconds per measure, then each note would sound for one second. The speed of the tempo determines the absolute duration of the sound of each note. Now, look at the third measure. The notes here are eighth notes, filled dots with flags on their stems or where the stems are connected as depicted here. Well, the eighth note lasts 1/8 the time it takes to constantly move left to right in a measure, fast or slow depending on tempo. In the third measure the four eighth notes together make up two beats, i.e., two quarter notes (1/8 * 4 = 1/4 * 2). Given a constant tempo, the eighth note will sound faster than the quarter note, twice as fast since it takes half the time to sound, i.e., 1/8 of the measure.